Introduction to Dynamic Programming

Dynamic programming mainly applied to optimization problems. So when we need to find out the optimal solution there we can use dynamic programming. There can be many other solutions, dynamic programming will help us to find out the optimal solution. Optimization problems are those which are required minimum results or maximum results, Shortest or Longest, etc.

Dynamic programming is like the divide-and-conquer method. It breaks down a complex problem into simple subproblems and find the optimal solution for the subproblems and conquer the solution of the subproblems and finally get the final solution. In contrast, dynamic programming is applicable when subproblems share subproblems that mean the same subproblems happened several times. A dynamic programming algorithm solves every subproblem only one time. It saves the answer and returns the saved answer next time when need to solve the same subproblems again. This is called memoization. 

So Dynamic programming follows the following steps to find out the optimal solution to a complex program. 

• Breaks down the complex problem into several sub-problems like the divide-and-conquer method.
• Find the optimal solution to these sub-problems.
• Store the result of sub-problems. It’s called memoization.
• Reuse the solutions of sub-problems so that the same sub-problem is not calculated more than once. 
• Finally, calculate the result of the complex problem.

The greedy method is also used to find out the optimal solution. But greedy can’t find out the option solution each time because the greedy method follows some specified procedure. On the other hand, dynamic programming finds out all possible solutions and peak up the optimal one. Dynamic programming is time-consuming compare to the greedy method but it guaranty that it will find out the optimal solution if the optimal solution exists. 

There are mainly two ways to solve a dynamic programming problem. 

1. Recursive formula with memoization
2. Tabular Folmula or Bottom-up approach

Mostly dynamic programming is solved with recursive formula. We will not use recursive programming but the formula is recursive. We solve it by iterative coding but the formula is recursive.

Example:

Find out the nth Fibonacci number. Fibonacci number of a position is equal to the summation of the previous two numbers Fibonacci. So Fibonacci of fib(n) is fib(n-1) + fib(n-1). 

Fibonacci of 6 is:

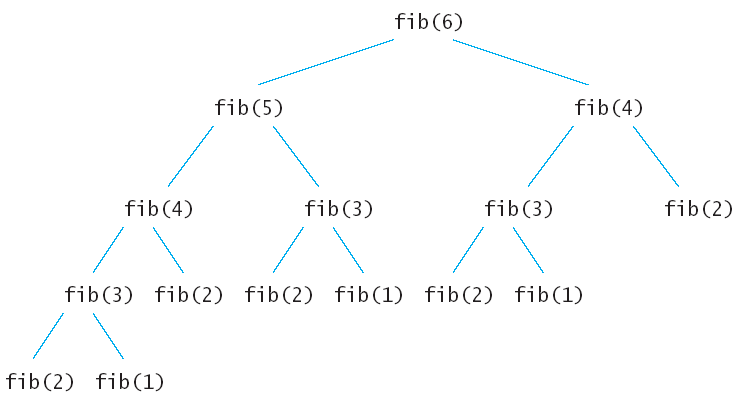
Here we divide the problem into several subproblems and conquer the result of the subproblems and finally get the optimal solution. But there is a problem that is here we are calculating a subproblem more than once. Here we calculate fib(4) twice, fib(3) three-time, fib(2) five times, fib(1) three times. Instead of calculating more than once we will store the solution of the subproblem and will use it for the next time.

Python Solution:

fib_data = [False] * (n + 1)

def fib(n):
    if fib_data[n]:
        return fib_data[n]
    if n in [1, 2]:
        return 1
    fib_data[n] = fib(n - 1) + fib(n - 2)
    return fib_data[n]

We can solve this problem using Boom-up approach:

fib_data = [False] * (n + 1)

def fib(n):
    fib_data[0] = 0
    fib_data[1] = 1
    for i in range(2, n + 1):
        fib_data[i] = fib_data[i - 1] + fib_data[i - 2]
    return fib_data[n]